Control theory is a branch of mathematics that deals with how to control a system. Control theory in robotics deals with the design of controllers for robots. A controller is the part of the system that receives external input and generates an output signal. The main idea of using control theory is to find a way to achieve a predefined goal for a system.

Control system block diagram
For example, let us say we are using a robot arm to open a door by applying pressure on the handle. We want to ensure that we apply the right amount of pressure to the handle to open it but not break it. This task might be obvious for a human but it is a tough challenge for a robotic system to handle.
Do you know that control theory played a central role in the rise of industrial robots over the past several decades and the original ideas are still relevant even today?
In this article, we will learn the very basics of control systems — open loop vs closed loop, feedback and feed-forward loops with some examples so that you will have a pretty good understanding of what these terms mean and how to proceed to explore more.
Open-loop: A system without feedback
In simple terms, an open-loop system is one without any feedback. It means the system receives inputs (say from sensors) and produces outputs (say motors). The output of the controller is given directly as the input to the system.
A simple example of an open-loop system is a motor that turns using a control knob. It can be a good or bad thing. It’s good that it is easy to set up, but if there is no resistance, the motor can easily turn too fast and overheat.

Open loop system block diagram
Simple robots are controlled using an open-loop technique. In open-loop control, you can see the results you get as soon as you activate the controls. There is no feedback from the system itself. However, when we control a complex system, such as a robot, open-loop control becomes impractical.
There are two main reasons why we need feedback in a system.
- Safety – In a system, if there is no feedback, then there is no way to determine whether or not the system is working properly. This could be because of a hardware failure, software bug, or just a user error. For example, if you are driving a car, you need feedback to tell you if you are going too fast or too slow. Without that feedback, you can’t tell how fast you are going which becomes a safety hazard.
- Efficiency – Feedback allows us to know what is going on, and this allows us to make decisions based on that information. Feedback allows us to learn from our mistakes. For example, if you are playing a game, you can learn how to play better by getting feedback from your mistakes. By learning, we can increase the efficiency of our system.
Closed-loop: A system with feedback
A closed-loop system is one in which the output of the system is fed back into the input.
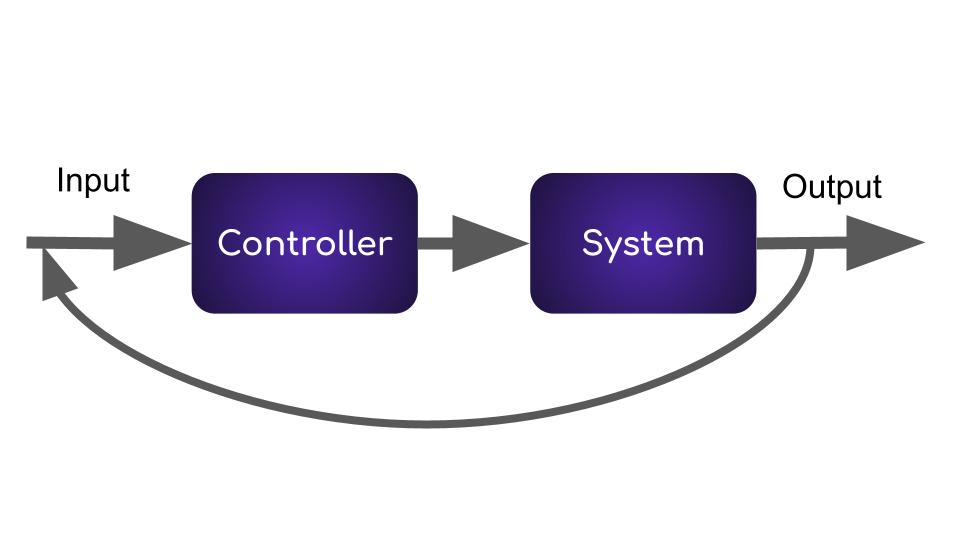
Closed loop system block diagram
An example of a closed loop system is a thermostat. When the temperature is low, the thermostat will turn on the heater and when the temperature is high, the thermostat will turn off the heater.
There are several benefits to using a closed-loop system, including being able to monitor and control the system from a single location. Closed-loop systems are much easier to maintain than open-loop systems.
Closed loop system can further be classified as feedback and feed-forward systems.
Feedback systems
In a traditional feedback system, the output is fed into the controller so that it can generate the desired output. In the thermostat example, the thermostat reads the temperature and compares it to the desired temperature. The difference is sent to the heater. This type of system works well for situations where the process can be modeled. For example, if you want a certain temperature at the beginning of a heating season, a closed-loop system can be designed to achieve this temperature.
Feed-forward-loop
If we have additional information about the system, we can use this information to set up a feed-forward loop. This additional information can come in the form of predictions about the system based on prior data or some external condition that occurs periodically. In the thermostat example, if we can sense the temperature outside then the heater can be turned on proactively even before the temperature inside the room drops before the set threshold.
This additional information is used to build a model of the system. A model of a system is a representation of the system that allows us to compute how the system will react given different inputs. This model is often an iterative approximation. If we can make a good guess as to how the system will react given a particular input, then we can improve the model and improve our guess as to how the system will react. This iterative process continues until the model predicts the behavior of the system accurately enough. Once the model is good enough, it can be used to predict the future state of the system (i.e., the future behavior of the temperature). This prediction can then be used to trigger a feed-forward response.
However, the model part can be very complex, particularly if we are dealing with nonlinear systems where the future behavior cannot be predicted reliably from the current state. So there may be a tradeoff between the amount of complexity of the model and the accuracy with which we can predict the future behavior of the system.
So the choice of feedback and feed-forward system depends on the problem we are trying to solve and how complex we want the model to be.
Control System Design
There are three main steps to a control process: modeling, simulation, and implementation. Modeling uses mathematical equations to represent a dynamic system. Simulation involves testing the system against different inputs and outputs. Finally, the implementation allows the real system to interact with its environment. This includes hardware design and the development of software for the controller to work with.
Modeling
A mathematical model is the first step in designing a control system. For example, if we want to make a system that will stabilize an unstable pendulum, we start by developing a mathematical model of the pendulum. From there, we use the model to predict what will happen when we change the position of the pendulum’s bob. Then we test our predictions to ensure that they match the actual results.
Simulation
After the mathematical model has been developed, we move on to simulation. In this phase, we test the system in the same way we would test the real-world system we’re modeling. We run our simulations hundreds or thousands of times to gain confidence that our mathematical model is accurate. The results from these tests can provide information about how the system will respond to different input signals. It can also be used to determine the correct parameters needed for the final implementation.
Implementation
After all of the simulation results have been gathered, we move on to the implementation phase. By now, we would have determined the correct values for our mathematical model and verified them with simulations. We finally implement the design in a real system. At this stage, the system is tested in a real-world environment. We may choose to change some of the values from the model or the simulation to match the real-world environment. We could also test the performance of the system under various conditions, such as temperature changes.
Conclusion
In conclusion, the control theory of robotics describes the behavior of robots in terms of their sensors, actuators, and controllers. An open-loop system operates without any feedback. Though it is easy to build, it is hard to control or get the desired behavior. A closed-loop system takes in feedback and can be used to control the system effectively. The feedback can be set up in two forms – feedback or feed-forward.
The feedback setup is a traditional setup where the output is fed back as input to the controller. If we have additional information about the system, we can create a model of the system and use that for predicting the behavior of the system. This can then be used to set up a feed-forward loop.
The process of control starts with the creation of a mathematical model of the system that is being controlled. The model is developed by first simulating the system in its environment. Next, the simulation results are used to create a simulation model that is used in the implementation stage. When implementing a new system, it is important to consider the consequences of using a given controller and compare the new results with simulations.



Use the share button below if you liked it.
It makes me smile, when I see it.